配送の最適化とはどんな技術か

現代社会では、荷物を届ける、逆に荷物を集める業務、即ち集配業務は基本的な物流インフラとして重要な位置を占めています。この集配業務を効率的に行なう為には、どの車両がどの集配先をどの様な順番でどの様な経路で回るのかに関する最適解を発見することが重要、必要です。この配送の最適解を自動的に精度良く実用的な応答速度で求めて提供するのが、配送の最適化です。

弊社では最適な配送計画を立案する配送計画エンジン「eCapOpt」を販売しています。また、eCapOptを体感して頂くためのASPサイト「簡単！配送計画サービス」を運用しています。是非こちらもご覧下さい。



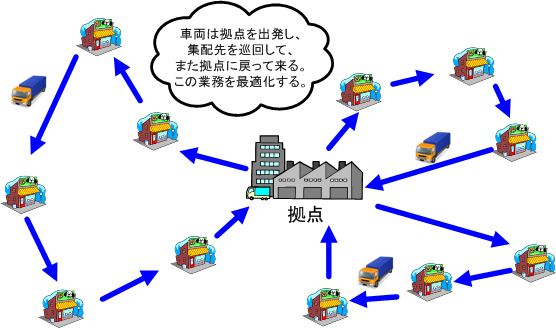
配送の最適化問題は以下の３つの部分最適化問題に分解出来ます。







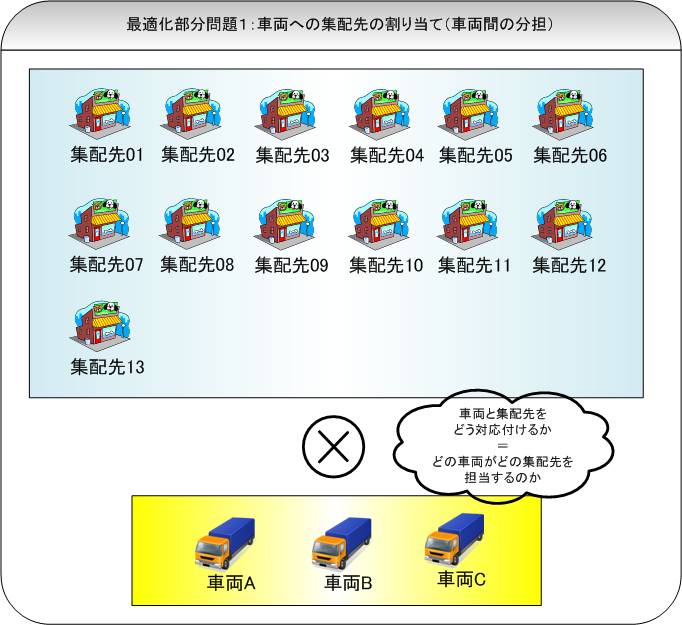
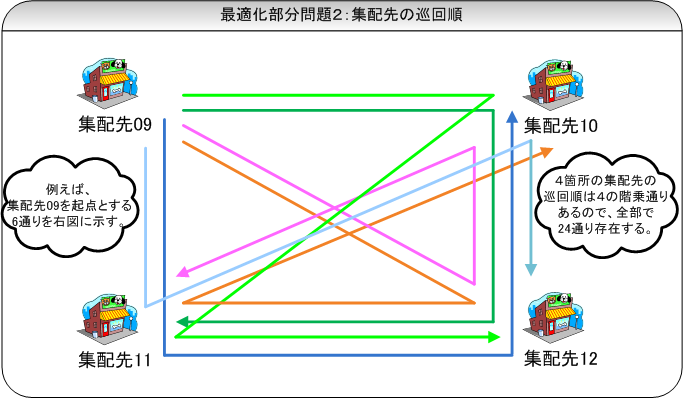
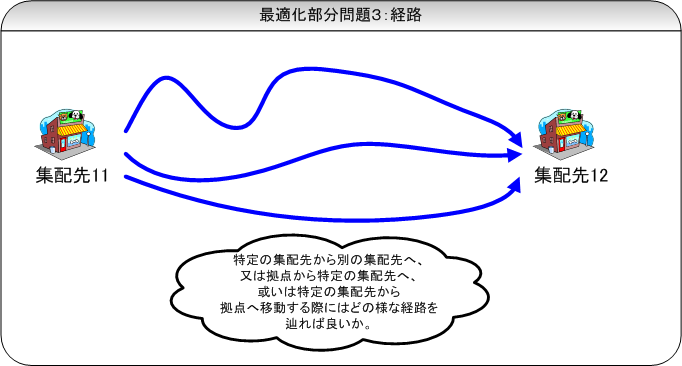
これらの部分最適化問題に対応する行動自体は御互いに独立した別々のものですが、実際に最適解を求める際には、部分最適化問題１~３は分離出来ず、つまり、例えば部分最適化問題１のみで解くことは出来ず、部分最適化問題１~３までの全ての解を求めた後に初めて、その解の最適解としてのレベル、満足度、正当性、或いは最適解か否かが判定出来る様になります。

配送の最適化はなぜ難しいのか

取り得る解の膨大さ

配送の最適化問題の解、即ち「どの車両がどの集配先をどの様な順番でどの様な経路で回るのか」と言う問いに対する答えは、現実には、膨大で天文学的な個数が存在することが一般的です。ほとんど無数にあるとすら言えます。具体的には、例えば１８個の集配先を３台の車両で分担して回る場合、以下の前提を置くと、取り得る解は18の階乗、即ちおよそ6424兆通り存在します。
（1）３台の車両は各々区別する。
（2）各々の車両の割り当てる集配先は、全て均等に６台とする。
（3）部分最適化問題１及び２まで考慮し部分最適化問題３は考慮しない。

３台の車両を区別しない（全て同じ車両とみなす）場合でも、およそ1067兆通り存在します。逆に、車両毎に割り当てられた集配先の個数として当初の（６，６，６）に加えて、（５，６，７）、（５，５，８）まで考慮すると、6424兆×3＝19207兆通りになります。実際には、集配先と拠点の配置によっては、（４，４，１０）、（４，５，９）、（４，６，８）等々も考慮しなければいけないし、更に部分最適化問題３の経路問題まで考慮すると可能解の個数が益々増えることは御理解頂けると思います。

応答性能の厳しさ

取り得る解が膨大にある割には、現実世界では、極めて短い時間で最適解を求めることが要求されます。長くても、数分、場合によっては数秒で。そこで取り得る解の膨大さを考慮すると、総当たり方式で最適解を求めることは到底出来ず、効率的に最適解を求める為の何らかのノウハウ、テクニック、方式が必要になることが分ります。

制約条件の多様さ、モデル化の難しさ

配送の最適化問題には、多くの場合、制約条件が付けられ、その制約条件の下で最適化問題を解くことが求められます。制約条件の一例を、下表に示しますが、これらはあくまで一例であって、現実社会では多様な制約条件が存在します。

項番	分類	名称	説明
1	集配先	訪問希望時刻開始	当該集配先には、例えば13:50から14:10までの間に行かなければいけないと言う訪問時刻の制約
2		訪問希望時刻終了
3		作業時間（集配先）	当該集配先では、荷物の積み込み、又は積み下しに例えば10分掛かると言う作業時間
4		作業時間（拠点）	当該集配先で積み込んだ又は積み下した荷物の為に、拠点で例えば12分掛かると言う作業時間
5		荷量	当該集配先で積み込んだ又は積み下ろす荷物の量
6		方面	主に集配先の位置関係に基づいて方面を導入し、互いに近い集配先、一緒に回った方が効率的である集配先同士をグルーピングしておく。
7		要員	荷物の積み下ろしに、誰に来て貰いたいのか、希望なり必須の要員がいれば、その要員を指定する。
8		位置	集配先の位置（座標や住所）
9	要員	勤務時刻開始	当該要員（運転手）は、例えば09:30から17:30の間しか働けないと言う勤務時刻の制約
10		勤務時刻終了
11		休憩の要不要	当該要員が休憩を必要とするか否か
12		休憩時間	当該要員が休憩を必要とする場合、例えば60分間と言う休憩時間
13		休憩可能時刻開始	当該要員が休憩を必要とする場合、例えば11:50から14:30までの間に休憩を取らなければいけないと言う休憩時刻の制約
14		休憩可能時刻終了
15	車両	積載可能荷量	当該車両には、例えば最大でどの位の荷物を積めるかと言う荷物の量の最大許容量
16	拠点	拠点位置	拠点の位置（座標や住所）

例えば項番5及び15には荷量と言う概念が出て来ますが、これは重さkgなのか大きさm3なのか、或いは両者かと言う問題が先ず考えられます。次に大きさで言うと、単に量だけではなく、それこそ、スペースの観点より「積めるのか無理か」問題に繋がり、これは寸法／形状の問題になります。寸法／形状の問題は、凝り始めたら、そのモデル化は相当複雑であることが御想像頂けるかと思います。
意外に厄介なのが休憩です。休憩はどこでも取って良いのか、拠点で必ず取らないといけないのか、集配先又は拠点の出発直後、或いは到着直後が最も望ましいのか、なども最適化問題を解く際には重要になります。
そもそも上記の要因は全て必要とは限らず、一部のみで良い場合もあり、また逆に不足している場合もあると思います。例えば、上記では要員と車両を分離していますが、これを一体化して捉える方がシンプルで運用し易いかも知れません。分離すると、例えば、１台の車両を運転する要員が午前と午後とで異なる、車両と要員の対応付けが固定化されない（例えば昨日と本日で、車両Ａを運転する要員が異なる）などの点で自由度は高くなります。反面、車両Ａを運転するのは必ず要員Ｐであるみたいな対応制約が掛け難くなります。項番6の方面は更に一歩進めると、車両なり要員と強制的に結び付けることも考えられますし、反面、方面など不要である、システムが提案する最適解こそが重要であると言う考えも有り得ると思います。

そもそも最適とは何か

そもそも最適解の最適とは何でしょうか。ちょっと考えるだけでも、例えば、以下が考えられます。現実世界で望まれているのは何なのでしょうか。この問い掛けより、最適化問題の複雑さをお感じ頂ければ幸いです。
（1）必要な車両台数を減らしたい。
（2）車両台数を増やしてでも、所定の時間内に必ず作業を終えたい。
（3）運用コストを削減したい。・・・では運用コストとは何でしょうか。

最適解をどう求めているのか

最適解を求めるとは

今、最適解を記述するための変量は２個であるとして、それを２次元平面上座標の（ｘ、ｙ）で表現します。この時、最適化の度合い（指標）をｚ座標で表現すると、解の最適化指標曲面のイメージは下図に示す通りであると考えられます。



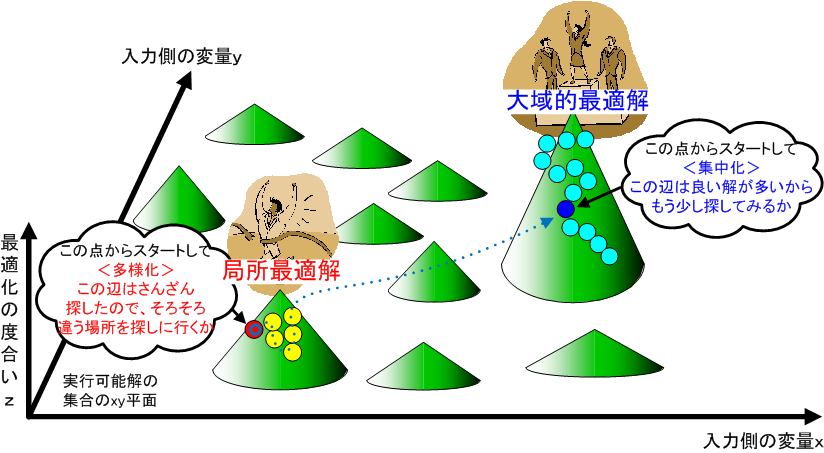
この時、最適解を求めることは、最大のｚを実現する（ｘ、ｙ）を求めることであると定義出来ます。但し、取り得る解（可能な解）の個数が膨大であるため、完全な最適解、即ちｚが最大である（ｘ、ｙ）と認められることは現実的には不可能であると考えられます。そこで、現実には、大域的最適解が求められた時点で満足する（その時点で打ち切る）ことが行われています。

一般論：必要な２つのこと

膨大な組み合わせの解が存在する場合、総当たり方式では、到底最適解は求められない、解空間の一部だけを探って、出来るだけ良い答えを探したいみたいな虫の良いことを考えた時に、どうすれば良いのか？どうも学術的には、図 2 3に示した２つの方針、即ち「集中化」と「多様化」の２つが回答であると考えているみたいです。以下にこの２種類の方針について説明します。

集中化(intensification)	良い解に近いところには良い解が存在するという性質(proximate optimality property)を信じて，良い解の回りを集中的に探索することである。
多様化(diversification)	悪い解のまわりで探索が停滞することを避けるために，今までに探索していない解を強制的に探索させること。局所最適解を避けるための考えである（以上、いずれも東京海洋大 久保　幹雄先生の定義）。

この２種類の方針は、その狙い、役割等の面で、お互いに真逆の位置を占めています。互いに正反対の機能を組み合わせて使うことで、より効果の高い最適解を求めることが出来ると考えたんでしょうね。その気持ちは分かりますね。実際問題として、これまでに研究されて来た方式の多くは、この２種類の方針のいずれか或いはいずれもを実現する様に工夫されています。

では現実の製品では？

当然のことですが、自社の最適化エンジンの実装方式は兎も角、他の企業の現実の製品がどう言う最適解探索方式を採用しているかは全くもって分りません。勿論、デモを拝見したり、カタログを見たりすれば、ある程度の推測は出来ますが、それはあくまで自分の頭で考えた推測であって、私の能力いや脳力を超えるアルゴリズムで動いていたら、当然のことながら、最早推測は出来ません。ただ、幾つかの製品を見て、また自身で配送の最適化エンジンを開発してみて、何となくハハンと感じる瞬間が時々あります。ここではその感じたことを記します。

大胆な絞り込み	製品の中にはあっという間に計算を終えてしまうものもあります。解の最適化度もそこそこありそうです。ところが、実際には、可能解のバリエーションは膨大にあるので、到底、実時間では全体を調べ切れない。これはどう考えれば良いのでしょうか。答えは、多分これが最適解であろうと言う解（正確には「最適解の候補」）を実行の早期に絞り込む、予想している、そしてそこにノウハウがある、そう言うことだと思います。
制約条件への対応	前項で言及した絞込みですが、場合によっては、制約条件の厳しさを見て、この場合はこう、あの場合はああ、と絞り込み方を変えている可能性があります。また、制約条件が変われば、結果的に絞り込む方式が変わることも有り得ると思います。要するに制約条件が変わればアルゴリズムも変わる、そう言う世界ではないかと感じます。
既存研究の有効性	論文に書かれている、言わば学術的な、或いは一般的な方法が正直どこまで、現実世界で有効なのかと疑問を感じています。と申しますのは、最適解については、制約条件を守ることが何より大切であるためです。制約条件を守ったままこれらの方法って適用出来るの？と疑問に思う方式が散見されます。なお、これは私の想像力が足りない為、そう考えるのであって、実際にはそんなことはないのかも知れない点は予めお詫びしておきます。

では弊社の製品では？

ここまで読まれた方は、「では御社（NCM）の製品ではどの様なアルゴリズムを採用しているの？」と問い質したいかも知れませんね。それについては、申し訳御座いません、結構、苦労して編み出した方式なので、余り確固たることは申し上げられないのですが、宣伝も兼ねて、特徴を以下の通り列挙します。
（1）制約条件を変更しても、追随し易い柔軟性を持たせる。
（2）解の絞込みを大胆に行ないつつ、局所解に陥らない様に配慮する。
（3）アイディアだけで勝負するのではなく、地道なパラメータチューニングにも注力する。

配車最適化エンジンへの入出力は何か

弊社の配車最適化エンジンへの入出力データを下表に示します。

項番	入力／出力の区別	分類	説明
1	入力	制約条件	「制約条件の多様さ、モデル化の難しさ」の表に一例を示した制約条件
2		道路ネットワーク	道路ネットワークデータ
3		パラメータ：道路ネットワーク関連	道路の走行速度、移動時間の割増率（移動に余裕を見るため）
4		パラメータ：損失コスト重み	制約条件が破綻した場合における損失コスト
5	出力	配送計画	どの車両がどの集配先をどの様な順番でどの様な経路で回るのか。どの車両をどの要員が運転するのか。
6		派生データ	例えば、拠点の出発／帰着時刻、集配先Ａの出発／到着時刻、或いはある集配先からその次の集配先までの走行時間／走行距離等の時刻と距離のデータ

最後に

弊社では最適な配送計画を立案する配送計画エンジン「eCapOpt」を販売しています。また、eCapOptを体感して頂くためのASPサイト「簡単！配送計画サービス」を運用しています。是非こちらもご覧下さい。

もし、このページに記載された技術へのニーズ、御興味を御持ちならば、是非とも、御連絡下さい。連絡先は、以下の通りです。
担当者：柳田
TEL ：03-6902-9701
E-Mail：yanagida@ncm-git.co.jp